Вот и добрались до сокращения. Применяется здесь основное свойство дроби. НО! Не всё так просто. Со многими дробями (в том числе из школьного курса) вполне можно им обойтись. А если взять дроби «покруче»? Разберём подробнее! Рекомендую посмотреть материалов с дробями.

Итак, мы уже знаем, что числитель и знаменатель дроби можно умножать и делить на одно и тоже число, дробь от этого не изменится. Рассмотрим три подхода:

Подход первый.

Для сокращения делят числитель и знаменатель на общий делитель. Рассмотрим примеры:

Сократим:

В приведенных примерах мы сразу видим какие взять делители для сокращения. Процесс несложен – мы перебираем 2,3.4,5 и так далее. В большинстве примеров школьного курса этого вполне достаточно. А вот если будет дробь:

Тут процесс с подбором делителей может затянуться надолго;). Конечно, такие примеры лежат вне школьного курса, но справляться с ними нужно уметь. Чуть ниже рассмотрим как это делается. А пока вернёмся к процессу сокращения.

Как рассмотрено выше, для того чтобы сократить дробь, мы осуществляли деление на определённый нами общий делитель(ли). Всё правильно! Стоит лишь добавить признаки делимости чисел:

— если число чётное то оно делится на 2.

— если число из последних двух цифр делится на 4, то и само число делится на 4.

— если сумма цифр из которых состоит число делится на 3, то и само число делится на 3. Например 125031, 1+2+5+0+3+1=12. Двенадцать делится на 3, значит и 123031 делится на 3.

— если в конце числа стоит 5 или 0, то число делится на 5.

— если сумма цифр из которых состоит число делится на 9, то и само число делится на 9. Например 625032 =.> 6+2+5+0+3+2=18. Восемнадцать делится на 9, значит и 623032 делится на 9.

Второй подход.

Если кратко суть, то на самом деле всё действо сводится к разложению числителя и знаменателя на множители и далее к сокращению равных множителей в числителе и знаменателе (данный подход – это следствие из первого подхода):

Визуально, чтобы не запутаться и не ошибиться равные множители просто перечёркивают. Вопрос – а как разложить число на множители? Нужно определить перебором все делители. Это тема отдельная, она несложная, посмотрите информацию в учебнике или интернете. Никаких великих проблем с разложением на множители чисел, которые присутствуют в дробях школьного курса, вы не встретите.

Формально принцип сокращения можно записать так:

Подход третий.

Тут самое интересное для продвинутых и тех, кто хочет им стать. Сократим дробь 143/273. Попробуйте сами! Ну и как, быстро получилось? А теперь смотрите!

Переворачиваем её (числитель и знаменатель меняем местами). Делим уголком полученную дробь переводим в смешанное число, то есть выделяем целую часть:

Уже проще. Мы видим, что числитель и знаменатель можно сократить на 13:

А теперь не забываем снова перевернуть дробь обратно, давайте запишем всю цепочку:

Проверено – времени уходит меньше, чем на перебор и проверку делителей. Вернёмся к нашим двум примерам:

Первый. Делим уголком (не на калькуляторе), получим:

Эта дробь попроще конечно, но с сокращением опять проблема. Теперь отдельно разбираем дробь 1273/1463, переворачиваем её:

Тут уже проще. Можем рассмотреть такой делитель как 19. Остальные не подходят, это видно: 190:19= 10, 1273:19 = 67. Ура! Запишем:

Следующий пример. Сократим 88179/2717.

Делим, получим:

Отдельно разбираем дробь 1235/2717, переворачиваем её:

Можем рассмотреть такой делитель как 13 (до 13 не подходят):

Числитель 247:13=19 Знаменатель 1235:13=95

*В процессе увидели ещё один делитель равный 19. Получается, что:

Теперь записываем исходное число:

И не важно, что будет больше в дроби – числитель или знаменатель, если знаменатель, то переворачиваем и действуем как описано. Таким образом мы можем сократить любую дробь, третий подход можно назвать универсальным.

Конечно, два примера рассмотренные выше это непростые примеры. Давайте попробуем эту технологию на уже рассмотренных нами «несложных» дробях:

Две четвёртых.

Семьдесят две шестидесятых. Числитель больше знаменателя, переворачивать не нужно:

Разумеется, третий подход применили к таким простым примерам просто как альтернативу. Способ, как уже сказано, универсальный, но не для всех дробей удобный и корректный, особенно это относится к простым.

Многообразие дробей велико. Важно, чтобы вы усвоили именно принципы. Строгого правила по работе с дробями просто нет. Посмотрели, прикинули каким образом удобнее действовать и вперёд. С практикой придёт навык и будете щёлкать их как семечки.

Вывод:

Если видите общий(ие) делитель(и) для числителя и знаменателя, то используйте их для сокращения.

Если умеете быстро раскладывать на множители число, то разложите числитель и знаменатель, далее сокращайте.

Если никак не можете определить общий делитель, то воспользуйтесь третьим подходом.

*Для сокращения дробей важно усвоить принципы сокращения, понимать основное свойство дроби, знать подходы к решению, быть крайне внимательным при вычислениях.

И запомните! Дробь принято сокращать до упора, то есть сокращать её пока есть общий делитель.

C уважением, Александр Крутицких.

В этой статье мы рассмотрим основные действия с алгебраическими дробями :

сокращение дробей
умножение дробей
деление дробей

Начнем с сокращения алгебраических дробей .

Казалось бы, алгоритм очевиден.

Чтобы сократить алгебраические дроби , нужно

1. Разложить числитель и знаменатель дроби на множители.

2. Сократить одинаковые множители.

Однако, школьники часто делают ошибку, "сокращая" не множители, а слагаемые. Например, есть любители, которые в дроби "сокращают" на и получают в результате , что, разумеется, неверно.

Рассмотрим примеры:

1. Сократить дробь:

1. Разложим на множители числитель по формуле квадрата суммы, а знаменатель по формуле разности квадратов

2. Разделим числитель и знаменатель на

2. Сократить дробь:

1. Разложим на множители числитель. Так как числитель содержит четыре слагаемых, применим группировку.

2. Разложим на множители знаменатель. Так же применим группировку.

3. Запишем дробь, которая у нас получилась и сократим одинаковые множители:

Умножение алгебраических дробей.

При умножении алгебраических дробей мы числитель умножаем на числитель, а знаменатель умножаем на знаменатель.

Важно! Не нужно торопиться выполнять умножение в числителе и знаменателе дроби. После того, как мы записали в числителе произведение числителей дробей, а в знаменателе - произведение знаменателей, нужно разложить на множители каждый множитель и сократить дробь.

Рассмотрим примеры:

3. Упростите выражение:

1. Запишем произведение дробей: в числителе произведение числителей, а в знаменателе произведение знаменателей:

2. Разложим каждую скобку на множители:

Теперь нам нужно сократить одинаковые множители. Заметим, что выражения и отличаются только знаком: и в результате деления первого выражения на второе получим -1.

Итак,

Деление алгебраических дробей мы выполняем по такому правилу:

То есть чтобы разделить на дробь, нужно умножить на "перевернутую".

Мы видим, что деление дробей сводится к умножению, а умножение, в конечном итоге, сводится к сокращению дробей.

Рассмотрим пример:

4. Упростите выражение:

Сокращение дробей нужно для того, чтобы привести дробь к более простому виду, например, в ответе полученном в результате решения выражения.

Сокращение дробей, определение и формула.

Что такое сокращение дробей? Что значит сократить дробь?

Определение:
Сокращение дробей – это разделение у дроби числитель и знаменатель на одно и то же положительное число не равное нулю и единице. В итоге сокращения получается дробь с меньшим числителем и знаменателем, равная предыдущей дроби согласно .

Формула сокращения дробей основного свойства рациональных чисел.

\(\frac{p \times n}{q \times n}=\frac{p}{q}\)

Рассмотрим пример:
Сократите дробь \(\frac{9}{15}\)

Решение:
Мы можем разложить дробь на простые множители и сократить общие множители.

\(\frac{9}{15}=\frac{3 \times 3}{5 \times 3}=\frac{3}{5} \times \color{red} {\frac{3}{3}}=\frac{3}{5} \times 1=\frac{3}{5}\)

Ответ: после сокращения получили дробь \(\frac{3}{5}\). По основному свойству рациональных чисел первоначальная и получившееся дробь равны.

\(\frac{9}{15}=\frac{3}{5}\)

Как сокращать дроби? Сокращение дроби до несократимого вида.

Чтобы нам получить в результате несократимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.

Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.

Получите несократимую дробь \(\frac{48}{136}\).

Решение:
Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НОД(48, 136)= 2⋅2⋅2=6

\(\frac{48}{136}=\frac{\color{red} {2 \times 2 \times 2} \times 2 \times 3}{\color{red} {2 \times 2 \times 2} \times 17}=\frac{\color{red} {6} \times 2 \times 3}{\color{red} {6} \times 17}=\frac{2 \times 3}{17}=\frac{6}{17}\)

Правило сокращения дроби до несократимого вида.

Нужно найти наибольший общий делитель для числители и знаменателя.
Нужно поделить числитель и знаменатель на наибольший общий делитель в результате деления получить несократимую дробь.

Пример:
Сократите дробь \(\frac{152}{168}\).

Решение:
Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НОД(152, 168)= 2⋅2⋅2=6

\(\frac{152}{168}=\frac{\color{red} {6} \times 19}{\color{red} {6} \times 21}=\frac{19}{21}\)

Ответ: \(\frac{19}{21}\) несократимая дробь.

Сокращение неправильной дроби.

Как сократить неправильную дробь?
Правила сокращения дробей для правильных и неправильных дробей одинаковы.

Рассмотрим пример:
Сократите неправильную дробь \(\frac{44}{32}\).

Решение:
Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.

\(\frac{44}{32}=\frac{\color{red} {2 \times 2 } \times 11}{\color{red} {2 \times 2 } \times 2 \times 2 \times 2}=\frac{11}{2 \times 2 \times 2}=\frac{11}{8}\)

Сокращение смешанных дробей.

Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.

Рассмотрим пример:
Сократите смешанную дробь \(2\frac{30}{45}\).

Решение:
Решим двумя способами:
Первый способ:
Распишем дробную часть на простые множители, а целую часть не будем трогать.

\(2\frac{30}{45}=2\frac{2 \times \color{red} {5 \times 3}}{3 \times \color{red} {5 \times 3}}=2\frac{2}{3}\)

Второй способ:
Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.

\(2\frac{30}{45}=\frac{45 \times 2 + 30}{45}=\frac{120}{45}=\frac{2 \times \color{red} {5 \times 3} \times 2 \times 2}{3 \times \color{red} {3 \times 5}}=\frac{2 \times 2 \times 2}{3}=\frac{8}{3}=2\frac{2}{3}\)

Вопросы по теме:
Можно ли сокращать дроби при сложении или вычитании?
Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:

Вычислите выражение \(\frac{50+20-10}{20}\) .

Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.

\(\frac{50+\color{red} {20}-10}{\color{red} {20}}=\frac{60}{20}=\frac{3 \times 20}{20}=\frac{3}{1}=3\)

На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь \(\frac{100}{150}\).

Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50

\(\frac{100}{150}=\frac{2 \times 50}{3 \times 50}=\frac{2}{3}\)

Получили несократимую дробь \(\frac{2}{3}\).

Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь \(\frac{100}{150}\) на 2.

\(\frac{100}{150}=\frac{2 \times 50}{2 \times 75}=\frac{50}{75}\)

Получили сократимую дробь \(\frac{50}{75}\).

Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac{4}{8}\). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.

Пример:
Сравните две дроби \(\frac{2}{3}\) и \(\frac{8}{12}\).

Эти две дроби равны. Рассмотрим подробно дробь \(\frac{8}{12}\):

\(\frac{8}{12}=\frac{2 \times 4}{3 \times 4}=\frac{2}{3} \times \frac{4}{4}=\frac{2}{3} \times 1=\frac{2}{3}\)

Отсюда получаем, \(\frac{8}{12}=\frac{2}{3}\)

Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.

Пример:
Сократите если возможно следующие дроби: а) \(\frac{90}{65}\) б) \(\frac{27}{63}\) в) \(\frac{17}{100}\) г) \(\frac{100}{250}\)

Решение:
а) \(\frac{90}{65}=\frac{2 \times \color{red} {5} \times 3 \times 3}{\color{red} {5} \times 13}=\frac{2 \times 3 \times 3}{13}=\frac{18}{13}\)
б) \(\frac{27}{63}=\frac{\color{red} {3 \times 3} \times 3}{\color{red} {3 \times 3} \times 7}=\frac{3}{7}\)
в) \(\frac{17}{100}\) несократимая дробь
г) \(\frac{100}{250}=\frac{\color{red} {2 \times 5 \times 5} \times 2}{\color{red} {2 \times 5 \times 5} \times 5}=\frac{2}{5}\)

С помощью дробей одну и ту же часть целого предмета можно записать разными способами.

На рисунке закрашена половина круга

Таким образом, все эти дроби равны.

Для удобства дополнительный множитель записывают на наклонной черте справа над дробью.

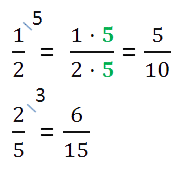
Вернёмся ещё раз к нашим дробям и запишем их в другом порядке.

Дробь, равную данной, можно получить, если числитель и знаменатель дроби одновременно разделить на одно и то же число, не равное нулю.

Такое преобразование дроби называют сокращением дроби .

Сокращение дроби обычно записывают следующим образом.

Числитель и знаменатель зачёркиваются чёрточками, и рядом с ними записываются результаты деления (частные) числителя и знаменателя на одно и то же число.

Число, на которое делили числитель и знаменатель, держим в уме.

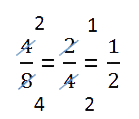
В нашем примере мы сокращали (то есть делили и числитель, и знаменатель) дробь на двойку, которую держали в уме.

Сокращение дроби можно проводить последовательно.

Основное свойство дроби

Сформулируем основное свойство дроби.

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.

Запишем это свойство в виде буквенных выражений.

, где « a », « b » и « k » - натуральные числа.

Сокращение дробей, правило и примеры сокращения дробей.

В этой статье мы подробно разберем, как проводится сокращение дробей . Сначала обговорим, что называют сокращением дроби. После этого поговорим о приведении сократимой дроби к несократимому виду. Дальше получим правило сокращения дробей и, наконец, рассмотрим примеры применения этого правила.

Навигация по странице.

Что значит сократить дробь?

Мы знаем, что обыкновенные дроби подразделяются на сократимые и несократимые дроби. По названиям можно догадаться, что сократимые дроби можно сократить, а несократимые – нельзя.

Что же значит сократить дробь? Сократить дробь – это значит разделить ее числитель и знаменатель на их положительный и отличный от единицы общий делитель. Понятно, что в результате сокращения дроби получается новая дробь с меньшим числителем и знаменателем, причем, в силу основного свойства дроби, полученная дробь равна исходной.

Для примера, проведем сокращение обыкновенной дроби 8/24 , разделив ее числитель и знаменатель на 2 . Иными словами, сократим дробь 8/24 на 2 . Так как 8:2=4 и 24:2=12 , то в результате такого сокращения получается дробь 4/12 , которая равна исходной дроби 8/24 (смотрите равные и неравные дроби). В итоге имеем .

Приведение обыкновенных дробей к несократимому виду

Обычно конечной целью сокращения дроби является получение несократимой дроби, которая равна исходной сократимой дроби. Эта цель может быть достигнута, если провести сокращение исходной сократимой дроби на наибольший общий делитель ее числителя и знаменателя. В результате такого сокращения всегда получается несократимая дробь. Действительно, дробь является несократимой, так как из свойств НОД известно, что и — взаимно простые числа. Здесь же скажем, что наибольший общий делитель числителя и знаменателя дроби является наибольшим числом, на которое можно сократить эту дробь.

Итак, приведение обыкновенной дроби к несократимому виду заключается в делении числителя и знаменателя исходной сократимой дроби на их НОД.

Разберем пример, для чего вернемся к дроби 8/24 и сократим ее на наибольший общий делитель чисел 8 и 24 , который равен 8 . Так как 8:8=1 и 24:8=3 , то мы приходим к несократимой дроби 1/3 . Итак, .

Заметим, что под фразой «сократите дробь» часто подразумевают приведение исходной дроби именно к несократимому виду. Другими словами, сокращением дроби очень часто называют деление числителя и знаменателя на их наибольший общий делитель (а не на любой их общий делитель).

Как сократить дробь? Правило и примеры сокращения дробей

Осталось лишь разобрать правило сокращения дробей, которое и объясняет, как сократить данную дробь.

Правило сокращения дробей состоит из двух шагов:

во-первых, находится НОД числителя и знаменателя дроби;
во-вторых, проводится деление числителя и знаменателя дроби на их НОД, что дает несократимую дробь, равную исходной.

Разберем пример сокращения дроби по озвученному правилу.

www.cleverstudents.ru

Сокращение дробей. Что значит сократить дробь?

Сокращение дробей, определение и формула.

Что такое сокращение дробей? Что значит сократить дробь?

Формула сокращения дробей основного свойства рациональных чисел.

Рассмотрим пример:
Сократите дробь \(\frac \)

Решение:
Мы можем разложить дробь на простые множители и сократить общие множители.

Ответ: после сокращения получили дробь \(\frac \). По основному свойству рациональных чисел первоначальная и получившееся дробь равны.

Как сокращать дроби? Сокращение дроби до несократимого вида.

Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.

Получите несократимую дробь \(\frac \).

Решение:
Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НОД(48, 136)= 2⋅2⋅2=6

Правило сокращения дроби до несократимого вида.

Нужно найти наибольший общий делитель для числители и знаменателя.
Нужно поделить числитель и знаменатель на наибольший общий делитель в результате деления получить несократимую дробь.

Пример:
Сократите дробь \(\frac \).

Решение:
Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НОД(152, 168)= 2⋅2⋅2=6

Ответ: \(\frac \) несократимая дробь.

Сокращение неправильной дроби.

Как сократить неправильную дробь?
Правила сокращения дробей для правильных и неправильных дробей одинаковы.

Рассмотрим пример:
Сократите неправильную дробь \(\frac \).

Решение:
Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.

Сокращение смешанных дробей.

Рассмотрим пример:
Сократите смешанную дробь \(2\frac \).

На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь \(\frac \).

Получили несократимую дробь \(\frac \).

Получили сократимую дробь \(\frac \).

Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac \). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.

Пример:
Сравните две дроби \(\frac \) и \(\frac \).

Эти две дроби равны. Рассмотрим подробно дробь \(\frac \):

Пример:
Сократите если возможно следующие дроби: а) \(\frac \) б) \(\frac \) в) \(\frac \) г) \(\frac \)

Действия с обыкновенными дробями

Расширение дроби. Сокращение дроби. Сравнение дробей.

Приведение к общему знаменателю. Сложение и вычитание дробей.

Умножение дробей. Деление дробей.

Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля расширением дроби . Например,

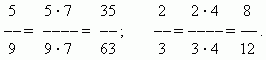
Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля . Это преобразование называется сокращением дроби . Например,

Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:

Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:

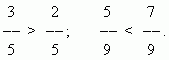
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.

П р и м е р. Сравнить две дроби:

Расширим первую дробь на знаменатель второй, а вторую — на знаменатель первой:

Использованное здесь преобразование называется приведением дробей к общему знаменателю .

Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.

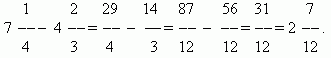
Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе .

П р и м е р.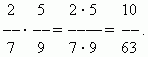

Деление дробей. Для того, чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь . Это правило вытекает из определения деления (см. раздел «Арифметические операции»).

П р и м е р.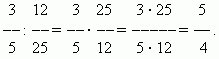

Умножение и деление дробей

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе - знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь - ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные - и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

Плюс на минус дает минус;
Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить - тот, которому не нашлось пары;
Если минусов не осталось, операция выполнена - можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение - весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей - это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Начальный уровень

Преобразование выражений. Подробная теория (2019)

Преобразование выражений

Часто мы слышим эту неприятную фразу: «упростите выражение». Обычно при этом перед нами какое-то страшилище типа этого:

«Да куда уж проще» - говорим мы, но такой ответ обычно не прокатывает.

Сейчас я научу тебя не бояться никаких подобных задач. Более того, в конце занятия ты сам упростишь этот пример до (всего лишь!) обычного числа (да-да, к черту эти буквы).

Но прежде чем приступить к этому занятию, тебе необходимо уметь обращаться с дробями и раскладывать многочлены на множители. Поэтому сперва, если ты этого не сделал раньше, обязательно освой темы « » и « ».

Прочитал? Если да, то теперь ты готов.

Базовые операции упрощения

Сейчас разберем основные приемы, которые используются при упрощении выражений.

Самый простой из них - это

1. Приведение подобных

Что такое подобные? Ты проходил это в 7 классе, как только впервые в математике появились буквы вместо чисел. Подобные - это слагаемые (одночлены) с одинаковой буквенной частью. Например, в сумме подобные слагаемые - это и.

Вспомнил?

Привести подобные - значит сложить несколько подобных слагаемых друг с другом и получить одно слагаемое.

А как же нам сложить друг с другом буквы? - спросишь ты.

Это очень легко понять, если представить, что буквы - это какие-то предметы. Например, буква - это стул. Тогда чему равно выражение? Два стула плюс три стула, сколько будет? Правильно, стульев: .

А теперь попробуй такое выражение: .

Чтобы не запутаться, пусть разные буквы обозначают разны предметы. Например, - это (как обычно) стул, а - это стол. Тогда:

стула стола стул столов стульев стульев столов

Числа, на которые умножаются буквы в таких слагаемых называются коэффициентами . Например, в одночлене коэффициент равен. А в он равен.

Итак, правило приведения подобных:

Примеры:

Приведите подобные:

Ответы:

2. (и подобны, так как, следовательно у этих слагаемых одинаковая буквенная часть).

2. Разложение на множители

Это обычно самая важная часть в упрощении выражений. После того как ты привел подобные, чаще всего полученное выражение нужно разложить на множители, то есть представить в виде произведения. Особенно это важно в дробях: ведь чтобы можно было сократить дробь, числитель и знаменатель должны быть представлены в виде произведения.

Подробно способы разложения выражений на множители ты проходил в теме « », поэтому здесь тебе остается только вспомнить выученное. Для этого реши несколько примеров (нужно разложить на множители):

Решения:

3. Сокращение дроби.

Ну что может быть приятнее, чем зачеркнуть часть числителя и знаменателя, и выбросить их из своей жизни?

В этом вся прелесть сокращения.

Все просто:

Если числитель и знаменатель содержат одинаковые множители, их можно сократить, то есть убрать из дроби.

Это правило вытекает из основного свойства дроби:

То есть суть операции сокращения в том, что числитель и знаменатель дроби делим на одно и то же число (или на одно и то же выражение).

Чтобы сократить дробь, нужно:

1) числитель и знаменатель разложить на множители

2) если в числителе и знаменателе есть общие множители , их можно вычеркнуть.

Принцип, я думаю, понятен?

Хочу обратить внимание на одну типичную ошибку при сокращении. Хоть эта тема и простая, но очень многие делают все неправильно, не понимая, что сократить - это значит поделить числитель и знаменатель на одно и то же число.

Никаких сокращений, если в числителе или знаменателе сумма.

Например: надо упростить.

Некоторые делают так: , что абсолютно неверно.

Еще пример: сократить.

«Самые умные» сделают так: .

Скажи мне, что здесь неверно? Казалось бы: - это множитель, значит можно сокращать.

Но нет: - это множитель только одного слагаемого в числителе, но сам числитель в целом на множители не разложен.

Вот другой пример: .

Это выражение разложено на множители, значит, можно сократить, то есть поделить числитель и знаменатель на, а потом и на:

Можно и сразу поделить на:

Чтобы не допускать подобных ошибок, запомни легкий способ, как определить, разложено ли выражение на множители:

Арифметическое действие, которое выполняется последним при подсчете значения выражения, является «главным». То есть, если ты подставишь вместо букв какие-нибудь (любые) числа, и попытаешься вычислить значение выражения, то если последним действием будет умножение - значит, у нас произведение (выражение разложено на множители). Если последним действием будет сложение или вычитание, это значит, что выражение не разложено на множители (а значит, сокращать нельзя).

Для закрепления реши самостоятельно несколько примеров :

Ответы:

1. Надеюсь, ты не бросился сразу же сокращать и? Еще не хватало «сократить» единицы типа такого:

Первым действием должно быть разложение на множители:

4. Сложение и вычитание дробей. Приведение дробей к общему знаменателю.

Сложение и вычитание обычных дробей - операция хорошо знакомая: ищем общий знаменатель, домножаем каждую дробь на недостающий множитель и складываем/вычитаем числители. Давай вспомним:

Ответы:

1. Знаменатели и - взаимно простые, то есть у них нет общих множителей. Следовательно, НОК этих чисел равен их произведению. Это и будет общий знаменатель:

2. Здесь общий знаменатель равен:

3. Здесь первым делом смешанные дроби превращаем в неправильные, а дальше - по привычной схеме:

Совсем другое дело, если дроби содержат буквы, например:

Начнем с простого:

a) Знаменатели не содержат букв

Здесь все то же, что и с обычными числовыми дробями: находим общий знаменатель, домножаем каждую дробь на недостающий множитель и складываем/вычитаем числители:

теперь в числителе можно приводить подобные, если есть, и раскладывать на множители:

Попробуй сам:

b) Знаменатели содержат буквы

Давай вспомним принцип нахождения общего знаменателя без букв:

· в первую очередь мы определяем общие множители;

· затем выписываем все общие множители по одному разу;

· и домножаем их на все остальные множители, не общие.

Чтобы определить общие множители знаменателей, сперва разложим их на простые множители:

Подчеркнем общие множители:

Теперь выпишем общие множители по одному разу и допишем к ним все необщие (не подчеркнутые) множители:

Это и есть общий знаменатель.

Вернемся к буквам. Знаменатели приводятся по точно такой же схеме:

· раскладываем знаменатели на множители;

· определяем общие (одинаковые) множители;

· выписываем все общие множители по одному разу;

· домножаем их на все остальные множители, не общие.

Итак, по порядку:

1) раскладываем знаменатели на множители:

2) определяем общие (одинаковые) множители:

3) выписываем все общие множители по одному разу и домножаем их на все остальные (неподчеркнутые) множители:

Значит, общий знаменатель здесь. Первую дробь нужно домножить на, вторую - на:

Кстати, есть одна хитрость:

Например: .

Видим в знаменателях одни и те же множители, только все с разными показателями. В общий знаменатель пойдут:

в степени

в степени.

Усложним задание:

Как сделать у дробей одинаковый знаменатель?

Давай вспомним основное свойство дроби:

Нигде не сказано, что из числителя и знаменателя дроби можно вычитать (или прибавлять) одно и то же число. Потому что это неверно!

Убедись сам: возьми любую дробь, например, и прибавь к числителю и знаменателю какое-нибудь число, например, . Что поучилось?

Итак, очередное незыблемое правило:

Когда приводишь дроби к общему знаменателю, пользуйся только операцией умножения!

Но на что же надо домножить, чтобы получить?

Вот на и домножай. А домножай на:

Выражения, которые невозможно разложить на множители будем называть «элементарными множителями». Например, - это элементарный множитель. - тоже. А вот - нет: он раскладывается на множители.

Что скажешь насчет выражения? Оно элементарное?

Нет, поскольку его можно разложить на множители:

(о разложении на множители ты уже читал в теме « »).

Так вот, элементарные множители, на которые ты раскладываешь выражение с буквами - это аналог простых множителей, на которые ты раскладываешь числа. И поступать с ними будем таким же образом.

Видим, что в обоих знаменателях есть множитель. Он пойдет в общий знаменатель в степени (помнишь, почему?).

Множитель - элементарный, и он у них не общий, значит первую дробь на него придется просто домножить:

Еще пример:

Решение:

Предже, чем в панике перемножать эти знаменатели, надо подумать, как их разложить на множители? Оба они представляют :

Отлично! Тогда:

Еще пример:

Решение:

Как обычно, разложим знаменатели на множители. В первом знаменателе просто выносим за скобки; во втором - разность квадратов:

Казалось бы, общих множителей нет. Но если присмотреться, то и так похожи… И правда:

Так и напишем:

То есть получилось так: внутри скобки мы поменяли местами слагаемые, и при этом знак перед дробью поменялся на противоположный. Возьми на заметку, так поступать придется часто.

Теперь приводим к общему знаменателю:

Усвоил? Сейчас проверим.

Задачи для самостоятельного решения:

Ответы:

Тут надо вспомнить еще одну - разность кубов:

Обрати внимание, что в знаменателе второй дроби не формула «квадрат суммы»! Квадрат суммы выглядел бы так: .

А - это так называемый неполный квадрат суммы: второе слагаемое в нем - это произведение первого и последнего, а не удвоенное их произведение. Неполный квадрат суммы - это один из множителей в разложени разности кубов:

Что делать, если дробей аж три штуки?

Да то же самое! В первую очередь сделаем так, чтобы максимальное количество множителей в знаменателях было одинаковым:

Обрати внимание: если поменять знаки внутри одной скобки, знак перед дробью меняется на противоположный. Когда меняем знаки во второй скобке, знак перед дробью снова меняется на противоположный. В результате он (знак перед дробью) не изменился.

В общий знаменатель выписавыем полностью первый знаменатель, а потом дописываем к нему все множители, которые еще не написаны, из второго, а потом из третьего (и так далее, если дробей больше). То есть получается вот так:

Хм… С дробями-то понятно что делать. Но вот как быть с двойкой?

Все просто: ты ведь умеешь складывать дроби? Значит, надо сделать так, чтобы двойка стала дробью! Вспоминаем: дробь - это операция деления (числитель делится на знаменатель, если ты вдруг забыл). И нет ничего проще, чем разделить число на. При этом само число не изменится, но превратится в дробь:

То, что нужно!

5. Умножение и деление дробей.

Ну что же, самое сложное теперь позади. А впереди у нас самое простое, но при этом самое важное:

Порядок действий

Какой порядок действий при подсчете числового выражения? Вспомни, посчитав значение такого выражения:

Посчитал?

Должно получиться.

Итак, напоминаю.

Первым делом вычисляется степень.

Вторым - умножение и деление. Если умножений и делений одновременно несколько, делать их можно в любом порядке.

И напоследок выполняем сложение и вычитание. Опять же, в любом порядке.

Но: выражение в скобках вычисляется вне очереди!

Если несколько скобок умножаются или делятся друг на друга, вычисляем сначала выражение в каждой из скобок, а потом умножаем или дели их.

А если внутри скобок есть еще одни скобки? Ну давай подумаем: внутри скобок написано какое-то выражение. А при вычислении выражения в первую очередь надо делать что? Правильно, вычислять скобки. Ну вот и разобрались: сначала вычисляем внутренние скобки, потом все остальное.

Итак, порядок действий для выражения выше такой (красным выделено текущее дествие, то есть действие, которое выполняю прямо сейчас):

Хорошо, это все просто.

Но это ведь не то же самое, что выражение с буквами?

Нет, это то же самое! Только вместо арифметических действий надо делать алгебраические, то есть действия, описанные в предыдущем разделе: приведение подобных , сложение дробей, сокращение дробей и так далее. Единственным отличием будет действие разложения многочленов на множители (его мы часто применяем при работе с дробями). Чаще всего для разложения на множители нужно применять я или просто выносить общий множитель за скобки.

Обычно наша цель - представить выражение в виде произведения или частного.

Например:

Упростим выражение.

1) Первым упрощаем выражение в скобках. Там у нас разность дробей, а наша цель - представить ее как произведение или частное. Значит, приводим дроби к общему знаменателю и складываем:

Больше это выражение упростить невозможно, все множители здесь - элементарные (ты еще помнишь, что это значит?).

2) Получаем:

Умножение дробей: что может быть проще.

3) Теперь можно и сократить:

Ну вот и все. Ничего сложного, правда?

Еще пример:

Упрости выражение.

Сначала попробуй решить сам, и уж только потом посмотри решение.

Перво-наперво определим порядок действий. Сначала выполним сложение дробей в скобках, получится вместо двух дробей одна. Потом выполним деление дробей. Ну и результат сложим с последней дробью. Схематически пронумерую действия:

Теперь покажу весть процесс, подкрашивая текущее действие красным:

Напоследок дам тебе два полезных совета:

1. Если есть подобные, их надо немедленно привести. В какой бы момент у нас ни образовались подобные, их желательно приводить сразу.

2. То же самое касается сокращения дробей: как только появляется возможность сократить, ей надо воспользоваться. Исключение составляют дроби, которые ты складываешь или вычитаешь: если у них сейчас одинаковые знаменатели, то сокращение нужно оставить на потом.

Вот тебе задачи для самостоятельного решения:

И обещанная в самом начале:

Решения (краткие):

Если ты справился хотя бы с первыми тремя примерами, то тему ты, считай, освоил.

Теперь вперед к обучению!

ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ

Базовые операции упрощения:

Приведение подобных : чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и приписать буквенную часть.
Разложение на множители: вынесение общего множителя за скобки, применение и т.д.
Сокращение дроби : числитель и знаменатель дроби можно умножать или делить на одно и то же ненулевое число, от чего величина дроби не изменяется.
1) числитель и знаменатель разложить на множители
2) если в числителе и знаменателе есть общие множители , их можно вычеркнуть.
ВАЖНО: сокращать можно только множители!
Сложение и вычитание дробей:
;
Умножение и деление дробей:
;